如图，在四边形中，AB||DCAD=√6，tan∠CAB=√2若AB=2√6，求△ABC的面积的最大值

更新时间2019-03-22 18:30:17

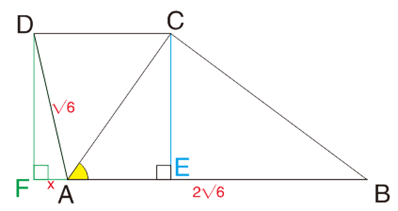
如图：AB=2√6

CE越大，△ABC面积越大。

DF=CE

DF≤AD

所以，当DF=AD时，△ABC面积越大。

S△ABC（最大）=√6×2√6÷2=6

本题：要求□ABCD的面积最大化，只有在AD⊥AB时，∠DAB=90°,

则：DC=AD时，四边形ABCD的面积最大。

S□ABCD=（AB+DC)*AD/2

=（2√6+√6）*√6/2

=3√6*√6/2

=3*6/2

=9

答案：□ABCD的面颊最大是9。

∵△ABC面积最大，∴C到AB的距离最大。

∵CD∥AB，∴D到AB的距离最大。∴DA⊥AB。

∴△ABC面积≤(1/2)DA*AB=(1/2)*√6*2√6=6。