长方形ABCD,AE=2厘米,DE=4厘米,∠BEC=120度,求三角形BCE的面积

更新时间2021-12-31 23:23:26

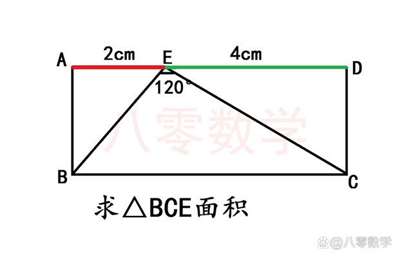
EB^2 = 2^2 + AB^2；

EC^2 = 4^2 + CD^2

由余弦定理，2EBECcos120° = EB^2 + EC^2 - BC^2

2 * ( -1/2 )√( 4 + AB^2 )√( 16 + AB^2 ) = 4 + AB^2 + 16 + AB^2 - ( 2 + 4 )^2

-√( 4 + AB^2 )√( 16 + AB^2 ) = 2AB^2 - 16

( 4 + AB^2 )( 16 + AB^2 ) = 4AB^4 - 64AB^2 + 256

AB^4 - 28AB^2 + 64 = 0

AB^2 = 14 ± 2√33；

经验证，AB^2 = 14 + 2√33 是增根；

故 AB^2 = 14 - 2√33，AB = √( 14 - 2√33 )；

三角形BCE的面积 S△BCE = AB * BC/2 = 3√( 14 - 2√33 ) 。